

The laws of compressible gas dynamics then accelerate the gases to supersonic speeds. After this point, the nozzle increases in area (diverges) and begins to expand the gas. This happens at the smallest area of the nozzle, the nozzle throat. With the (now) fixed equation, the exit Mach is 3.28, the exit static temperature is 2,100 K, and the exit velocity is 3,120 m/s. The nozzle converges until the gases become sonic, or in other words, until they reach mach 1.

The merlin engine's exit pressure is much lower for optimized performance at higher altitudes.ĮDIT: I forgot to subtract the 1 in the Mach from pressure ratio equation. pressure, velocity, etc.) are uniform at any point in the flow direction, thrust is simply the gas momentum at the nozzle exit, minus the influence of pressure. The surplus of thrust is likely due to the unrealistic exit pressure of 1 atm. Plugging mass flow and exit velocity into the thrust equation gives a thrust of 994 kN! Which is pretty close to the vacuum thrust of the actual merlin engine (981 kN). The equations I used are the most commonly taught compressible isentropic flow equations and can all be found on the NASA GRC Website.įollowing my solution, I compute a mass flow of 262 kg/s, an exit Mach number of 5, an exit static temperature of 1,340 K, and an exit velocity of 3,800 m/s. Now you can plug the exit Mach and static temperature into the equation for exit velocity and wam bam you thrustin boi. in or out of exhaust gases leaving the outlet to vary the configuration of the final. Here, $V_e$ is the nozzle exit velocity, $\dot$$ A conventional variable area thrust nozzle for a gas turbine jet.
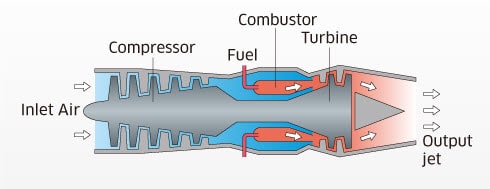
You should start with the thrust equation for a rocket engine: You also need to check your equations as they all seem a little screwy for rocket science. All the thrust of a turbojet engine is due to the exhaust gases leaving the engine at about twice the speed of sound. You have a lot of powerful information in that table.


 0 kommentar(er)
0 kommentar(er)
